Canopy Density Estimation Model in Peat Swamp Forest Using LiDAR Data and Landsat 8 OLI Satellite Imagery
Abstract
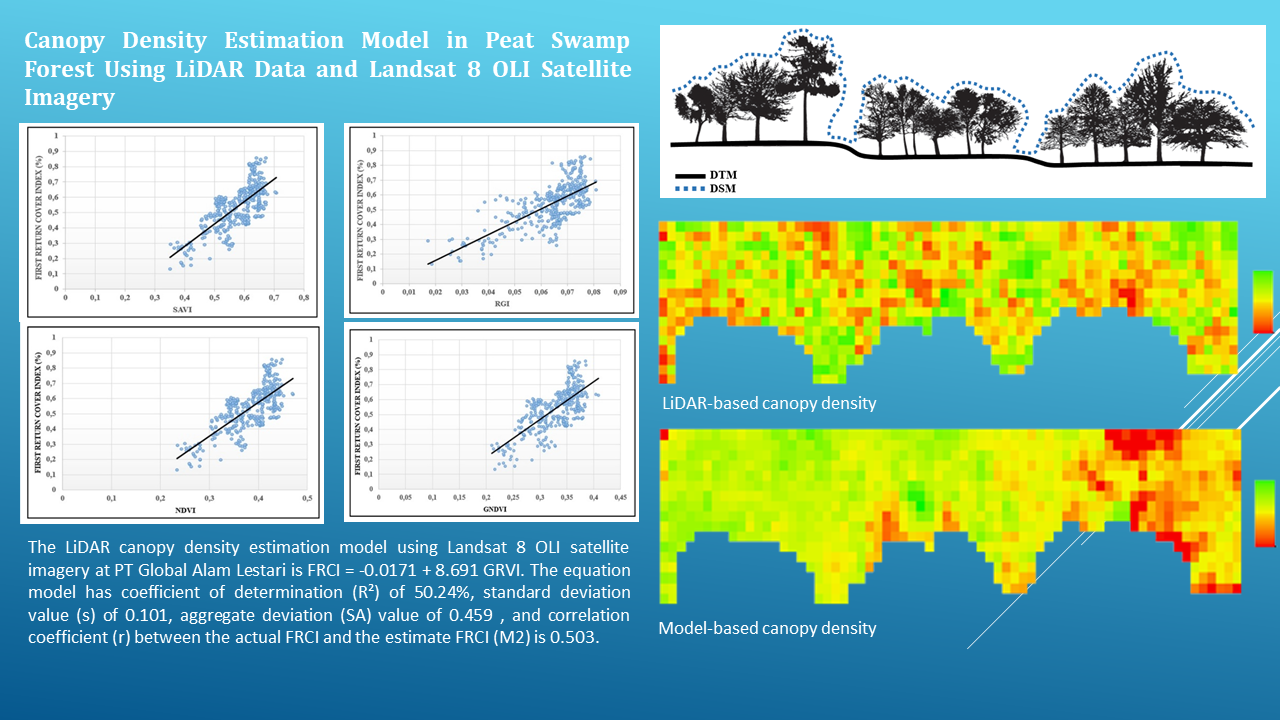
Canopy density is one of the important parameters in measuring the forest conditions. Canopy density can be estimated by using a remote sensing technology system. Light Detection and Ranging (LiDAR) is an active remote sensing system which uses a laser that is emitted by a sensor to the objects on the earth surface. For a wide area, image utilization which solely relies on LiDAR is still relatively expensive, so it is necessary to develop a method that combine LiDAR data with other medium resolution images such as Landsat 8 OLI imagery. Therefore, this research was conducted to obtain the canopy density estimation model from LiDAR and Landsat 8 OLI data. The results showed that the best estimation model at the study site, PT Global Alam Lestari's peat swamp forest was FRCI = - 0.0171 + 8.691 GRVI. The equation model had coefficient of determination (R²) of 50.2%, standard deviation value (s) of 0.101, aggregate deviation (SA) value of 0.459, and correlation coefficient (r) between the actual FRCI and the estimation FRCI (best model) of 0.503.
References
Priyanto Model Penduga Biomassa Tegakan Hutan Rawa Gambut Menggunakan Citra SPOT Pankromatik [Tesis]; IPB Press: Bogor, 2011;
Lu, D. The Potential and Challenge of Remote Sensing-Based Biomass Estimation. Int J Remote Sens 2006, 27, 1297–1328.
Prahasta, E. Pengolahan Data Sistem LiDAR (Light Detection and Ranging) Di Bidang Teknik Geodesi Dan Geomatika; Informatika Bandung: Bandung, 2015;
Jaya, I.N.S. Analisis Citra Digital: Perspektif Penginderaan Jauh Untuk Pengelolaan Sumberdaya Alam; Fakultas Kehutanan IPB: Bogor, 2010;
Korhonen, L.; Korpela, I.; Heiskanen, J.; Maltamo, M. Airborne Discrete-Return LiDAR Data in the Estimation of Vertical Canopy Cover, Angular Canopy Closure and Leaf Area Index. Journal of Remote Sensing of Environment 2011, 115, 1065–1080.
Ma, Q.; Su, Y.; Guo, Q. Comparison of Canopy Cover Estimation from Airborne LiDAR, Aerial Imagery, and Satellite Imagery. Journal of Selected Topic in Applied Earth Observations and Remote Sensing 2017, 10, 4225–4236.
Mahecha, M.D.; Martínez, A.; Lischeid, G.; Beck, E. Nonlinear Dimensionality Reduction: Alternative Ordination Approaches for Extracting and Visualizing Biodiversity Patterns in Tropical Montane Forest Vegetation Data. Ecological Informatics 2007, 2, 138–149, doi:10.1016/J.ECOINF.2007.05.002.
Zhao, N.; Xu, Q.; Tang, M.L.; Jiang, B.; Chen, Z.; Wang, H. High-Dimensional Variable Screening under Multicollinearity. Stat 2020, 9, doi:10.1002/sta4.272.
Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A Review of Methods to Deal with It and a Simulation Study Evaluating Their Performance. Ecography 2013, 36, doi:10.1111/j.1600-0587.2012.07348.x.
Toothaker, L.E.; Aiken, L.S.; West, S.G. Multiple Regression: Testing and Interpreting Interactions. The Journal of the Operational Research Society 1994, 45, doi:10.2307/2583960.
Farrar, D.E.; Glauber, R.R. Multicollinearity in Regression Analysis: The Problem Revisited. The Review of Economics and Statistics 1967, 49, doi:10.2307/1937887.
O’Brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Quality and Quantity 2007, 41, doi:10.1007/s11135-006-9018-6.
Tu, Y.K.; Clerehugh, V.; Gilthorpe, M.S. Collinearity in Linear Regression Is a Serious Problem in Oral Health Research. European Journal of Oral Sciences 2004, 112.
Graham, M.H. Confronting Multicollinearity in Ecological Multiple Regression. Ecology 2003, 84, doi:10.1890/02-3114.
Mason, C.H.; Perreault, W.D. Collinearity, Power, and Interpretation of Multiple Regression Analysis. Journal of Marketing Research 1991, 28, doi:10.2307/3172863.
Fekedulegn, B.D.; Colbert, J.J.; Hicks, R.R.; Schuckers, M.E.; Service, F.; Fekedulegn, B.D.; Colbert, J.J.; Hicks, R.R.; Schuckers, M.E. Coping with Multicollinearity : An Example on Application of Principal Components Regression in Dendroecology. United States Department of Agriculture 2002.
Stewart, G.W. Collinearity and Least Squares Regression. Statistical Science 1987, 2, doi:10.1214/ss/1177013439.
Gordon, R.A. Issues in Multiple Regression. American Journal of Sociology 1968, 73, doi:10.1086/224533.
Feng, X.; Park, D.S.; Walker, C.; Peterson, A.T.; Merow, C.; Papeş, M. A Checklist for Maximizing Reproducibility of Ecological Niche Models. Nature Ecology & Evolution 2019, 3, 1382–1395, doi:10.1038/s41559-019-0972-5.
Tiryana, T. Panduan Praktis Analisis Regresi Linear Dengan Program Minitab For Windows; Fakultas Kehutanan IPB: Bogor, 2008;
Santi, R.C.N.; Eniyati, S. Implementasi Statistic Dengan Database Mysql. Jurnal Teknologi Informasi DINAMIK 2015, 20, 132–139.
Draper, N.R.; Smith, H. Analisis Regresi Terapan Edisi 2 Terjemahan; Gramedia: Jakarta, 1992;
Maubanu, E.; Kartiko Analisis Komponen Utama Untuk Mengatasi Multikolinearitas Pada Faktor-Faktor Yang Mempengaruhi Tingkat Pengangguran Terbuka Di Provinsi Nusa Tenggara Timur. Jurnal Statistik Industri dan Komputasi 2018, 3, 21–30.
Authors

This work is licensed under a Creative Commons Attribution 4.0 International License.
Media Konservasi is an open access journal, meaning that all content is freely available without charge to the user or their institution. Users are allowed to read, download, copy, distribute, print, search, or link to the full texts of the articles in this journal without needing to request prior permission from the publisher or the author.
All articles published by Media Konservasi are licensed under the Creative Commons Attribution 4.0 International License. This allows for unrestricted use, distribution, and reproduction in any medium, provided proper credit is given to the original authors.
Authors submitting manuscripts should understand and agree that the copyright of published manuscripts is retained by the authors. Copyright encompasses the exclusive rights of authors to reproduce, distribute, and sell any part of the journal articles in all forms and media. Reproduction of any part of this journal, its storage in databases, and its transmission by any form or media is allowed without written permission from Media Konservasi.